Chapter 9 Inference for Regression

In this chapter, we’ll further explore the regression models we first studied in Chapter 8. Armed with our knowledge of confidence intervals and hypothesis tests from Chapters 6 and 7, we’ll be able to apply statistical inference to further our understanding of relationships between outcome and explanatory variables.

Chapter Learning Objectives

At the end of this chapter, you should be able to…
• Fully interpret a regression table to determine the p-value and 95% confidence interval of the point estimates for the intercept and slope of the regression line.
• Check if data meets the necessary conditions to apply linear regression.

Needed packages

Let’s load all the packages needed for this chapter (this assumes you’ve already installed them). Recall from our discussion in Section 4.3 that loading the tidyverse package by running library(tidyverse) loads the following commonly used data science packages all at once:

• ggplot2 for data visualization
• dplyr for data wrangling
• tidyr for converting data to “tidy” format
• readr for importing spreadsheet data into R
• As well as the more advanced purrr, tibble, stringr, and forcats packages

If needed, read Section 1.3 for information on how to install and load R packages.

library(tidyverse)
library(moderndive)
library(infer)
library(abd)

9.1 Regression refresher

Before jumping into inference for regression, let’s remind ourselves of the study to estimate nose coloration based on lion ages in Section 8.1.

9.1.1 Lion age and nose coloration

Recall using simple linear regression we modeled the relationship between

1. A numerical outcome variable \(y\) (proportion of the nose that’s black) and
2. A single numerical explanatory variable \(x\) (lion’s age).

We started with the LionNoses data frame in the abd package, which contained the two variables of interest: age and proportion.black:

glimpse(LionNoses)

Rows: 32
Columns: 2
$ age              <dbl> 1.1, 1.5, 1.9, 2.2, 2.6, 3.2, 3.2, 2.9, 2.4, 2.1, 1.9…
$ proportion.black <dbl> 0.21, 0.14, 0.11, 0.13, 0.12, 0.13, 0.12, 0.18, 0.23,…

In Subsection 8.1.1, we performed an exploratory data analysis of the relationship between these two variables of age and proportion.black. We saw there that a clearly positive correlation of 0.79 existed between the two variables.

This was evidenced in Figure 9.1 of the scatterplot along with the “best-fitting” regression line that summarizes the linear relationship between the two variables of proportion.black and age. Recall in Subsection 8.3.2 that we defined a “best-fitting” line as the line that minimizes the sum of squared residuals.

ggplot(LionNoses, 
       aes(x = age, y = proportion.black)) +
  geom_point() +
  labs(x = "Age (years)", 
       y = "Proportion of black nose",
       title = "Scatterplot of relationship of relative coloration and age of male lions.") +  
  geom_smooth(method = "lm", se = FALSE)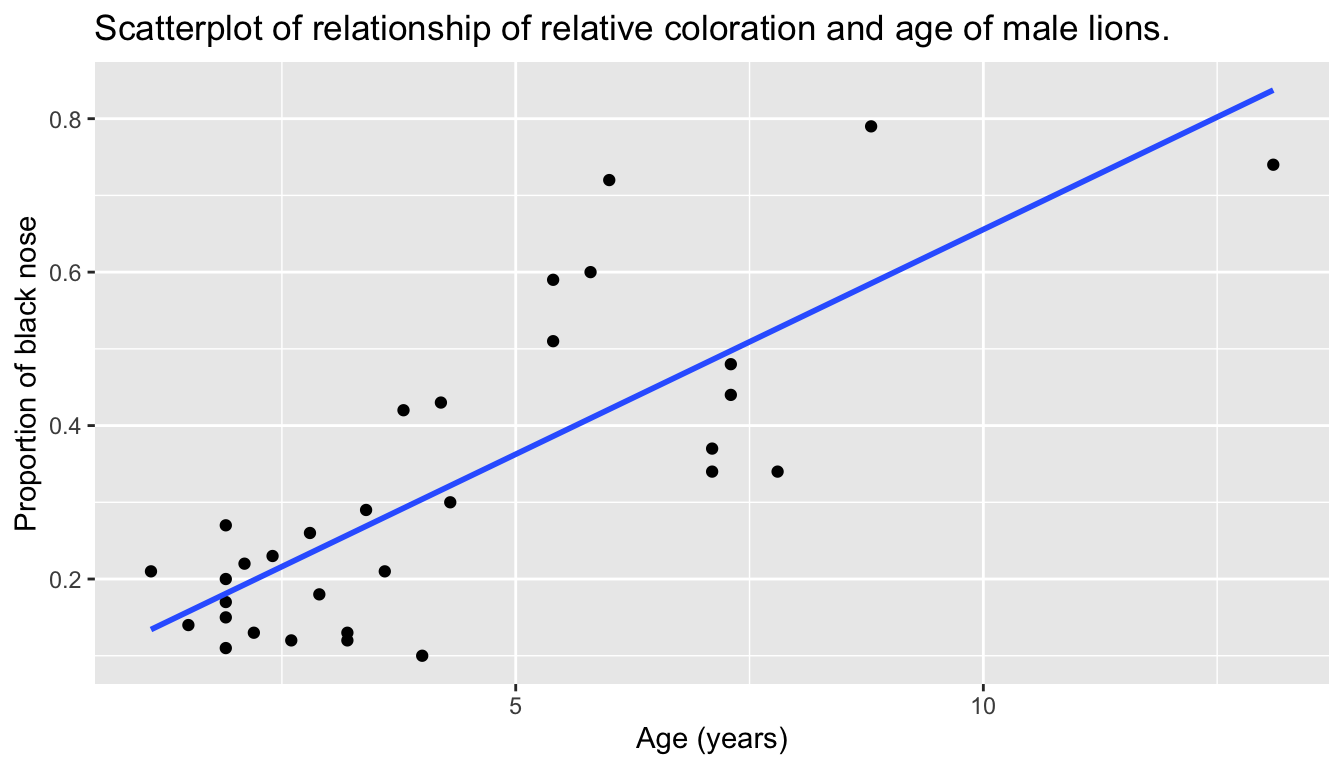

FIGURE 9.1: Relationship with regression line.

Looking at this plot again, you can see that the line has a positive slope, increasing from left to right as the age variable increases, but by how much? To get to this information, recall that we followed a two-step procedure:

1. We first “fit” the linear regression model using the lm() function with the formula proportion.black ~ age. We saved this model in lion_model.
2. We get the regression table by applying the get_regression_table() function from the moderndive package to lion_model.

# Fit regression model:
lion_model <- lm(proportion.black ~ age, data = LionNoses)
# Get regression table:
get_regression_table(lion_model)

TABLE 9.1: Previously seen linear regression table

term	estimate	std_error	statistic	p_value	lower_ci	upper_ci
intercept	0.070	0.042	1.66	0.107	-0.016	0.155
age	0.059	0.008	7.05	0.000	0.042	0.076

Using the values in the estimate column of the resulting regression table in Table 9.1, we could then obtain the equation of the “best-fitting” regression line in Figure 9.1:

\[ \begin{aligned} \widehat{y} &= b_0 + b_1 \cdot x\\ \widehat{\text{proportion.black}} &= b_0 + b_{\text{age}} \cdot\text{age}\\ &= 0.070 + 0.059\cdot\text{age} \end{aligned} \]

where \(b_0\) is the fitted intercept and \(b_1\) is the fitted slope for age. Recall the interpretation of the \(b_1\) = 0.059 value of the fitted slope:

For every increase of one unit in lion age, there is an associated increase, on average, of 0.059 units of the black proportion of the nose.

Thus, the slope value quantifies the relationship between the \(y\) variable proportion.black and the \(x\) variable age. We also discussed the intercept value of \(b_0\) = 0.07 and its lack of practical interpretation, since the range of ages doesn’t include 0.

9.1.2 Sampling scenario

Let’s now revisit this study in terms of the terminology and notation related to sampling we studied in Subsection 5.3.1.

First, let’s view these 32 lions as a representative sample from a greater study population. In our case, let’s assume that the study population is all lions living in the wild and that this sample of 32 lions is a representative sample. Unfortunately, we can only assume these two facts without more knowledge of the sampling methodology used by the researchers.

Since we are viewing these \(n\) = 32 lions as a sample, we can view our fitted slope \(b_1\) = 0.059 as a point estimate of the population slope \(\beta_1\). In other words, \(\beta_1\) quantifies the relationship between proportion.black and age for all lions in the wild. Similarly, we can view our fitted intercept \(b_0\) = 0.07 as a point estimate of the population intercept \(\beta_0\) for all lions in the wild.

Putting these two ideas together, we can view the equation of the fitted line \(\widehat{y}\) = \(b_0 + b_1 \cdot x\) = \(0.070 + 0.059 \cdot \text{age}\) as an estimate of some true and unknown population line \(y = \beta_0 + \beta_1 \cdot x\). Thus we can draw parallels between our lion age analysis and all the sampling scenarios we’ve seen previously. In this chapter, we’ll focus on the final scenario of regression slopes as shown in Table 9.2.

TABLE 9.2: Scenarios of sampling for inference

Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	\(p\)	Sample proportion	\(\widehat{p}\)
2	Population mean	\(\mu\)	Sample mean	\(\overline{x}\) or \(\widehat{\mu}\)
3	Difference in population proportions	\(p_1 - p_2\)	Difference in sample proportions	\(\widehat{p}_1 - \widehat{p}_2\)
4	Difference in population means	\(\mu_1 - \mu_2\)	Difference in sample means	\(\overline{x}_1 - \overline{x}_2\)
5	Population regression slope	\(\beta_1\)	Fitted regression slope	\(b_1\) or \(\widehat{\beta}_1\)

Since we are now viewing our fitted slope \(b_1\) and fitted intercept \(b_0\) as point estimates based on a sample, these estimates will again be subject to sampling variability. In other words, if we collected a new sample of data on a different set of \(n\) = 32 lions, the new fitted slope \(b_1\) will likely differ from 0.059. The same goes for the new fitted intercept \(b_0\). But by how much will these estimates vary? This information is in the remaining columns of the regression table in Table 9.1. Our knowledge of sampling from Chapter 5, confidence intervals from Chapter 6, and hypothesis tests from Chapter 7 will help us interpret these remaining columns.

9.2 Interpreting regression tables

We’ve so far focused only on the two leftmost columns of the regression table in Table 9.1: term and estimate. Let’s now shift our attention to the remaining columns: std_error, statistic, p_value, lower_ci and upper_ci in Table 9.3.

TABLE 9.3: Previously seen regression table

term	estimate	std_error	statistic	p_value	lower_ci	upper_ci
intercept	0.070	0.042	1.66	0.107	-0.016	0.155
age	0.059	0.008	7.05	0.000	0.042	0.076

Given the lack of practical interpretation for the fitted intercept \(b_0\), in this section we’ll focus only on the second row of the table corresponding to the fitted slope \(b_1\). We’ll first interpret the std_error, statistic, p_value, lower_ci and upper_ci columns. Afterwards in the upcoming Subsection 9.2.5, we’ll discuss how R computes these values.

9.2.1 Standard error

The third column of the regression table in Table 9.1 std_error corresponds to the standard error of our estimates. Recall the definition of standard error we saw in Subsection 5.3.2:

The standard error is the standard deviation of any point estimate computed from a sample.

So what does this mean in terms of the fitted slope \(b_1\) = 0.059? This value is just one possible value of the fitted slope resulting from this particular sample of \(n\) = 32 pairs of black proportions and ages. However, if we collected a different sample of \(n\) = 32 pairs of black proportions and ages, we will almost certainly obtain a different fitted slope \(b_1\). This is due to sampling variability.

Say we hypothetically collected 1000 such samples of pairs of black proportions and ages, computed the 1000 resulting values of the fitted slope \(b_1\), and visualized them in a histogram. This would be a visualization of the sampling distribution of \(b_1\), which we defined in Subsection 5.3.2. Further recall that the standard deviation of the sampling distribution of \(b_1\) has a special name: the standard error.

Recall that we constructed three sampling distributions for the sample proportion \(\widehat{p}\) using shovels of size 25, 50, and 100 in Figure 5.13. We observed that as the sample size increased, the standard error decreased as evidenced by the narrowing sampling distribution.

The standard error of \(b_1\) similarly quantifies how much variation in the fitted slope \(b_1\) one would expect between different samples. So in our case, we can expect about 0.008 units of variation in the age slope variable. Recall that the estimate and std_error values play a key role in inferring the value of the unknown population slope \(\beta_1\) relating to all lions.

In Section 9.4, we’ll perform a simulation using the infer package to construct the bootstrap distribution for \(b_1\) in this case. Recall from Subsection 6.7 that the bootstrap distribution is an approximation to the sampling distribution in that they have a similar shape. Since they have a similar shape, they have similar standard errors. However, unlike the sampling distribution, the bootstrap distribution is constructed from a single sample, which is a practice more aligned with what’s done in real life.

9.2.2 Test statistic

The fourth column of the regression table in Table 9.1, statistic, corresponds to a test statistic relating to the following hypothesis test:

\[ \begin{aligned} H_0 &: \beta_1 = 0\\ \text{vs } H_A&: \beta_1 \neq 0. \end{aligned} \]

Recall our terminology, notation, and definitions related to hypothesis tests we introduced in Section 7.2.

A hypothesis test consists of a test between two competing hypotheses: (1) a null hypothesis \(H_0\) versus (2) an alternative hypothesis \(H_A\).

A test statistic is a point estimate/sample statistic formula used for hypothesis testing.

Here, our null hypothesis \(H_0\) assumes that the population slope \(\beta_1\) is 0. If the population slope \(\beta_1\) is truly 0, then this is saying that there is no true relationship between the black nose proportion and age for all lions in our population. In other words, \(x\) = age would have no associated effect on \(y\) = proportion.black. The alternative hypothesis \(H_A\), on the other hand, assumes that the population slope \(\beta_1\) is not 0, meaning it could be either positive or negative. This suggests either a positive or negative relationship between black nose proportion and lion age. Recall we called such alternative hypotheses two-sided. By convention, all hypothesis testing for regression assumes two-sided alternatives.

Recall our “hypothesized universe” of no effect of egg removal we assumed in our BirdMalaria activity in Section 7.1. Similarly here when conducting this hypothesis test, we’ll assume a “hypothesized universe” where there is no relationship between black nose proportion and lion age. In other words, we’ll assume the null hypothesis \(H_0: \beta_1 = 0\) is true.

The statistic column in the regression table is a tricky one, however. It corresponds to a standardized t-test statistic, much like the two-sample \(t\) statistic we saw in Subsection 7.6 where we used a theory-based method for conducting hypothesis tests. In both these cases, the null distribution can be mathematically proven to be a \(t\)-distribution. Since such test statistics are tricky for individuals new to statistical inference to study, we’ll skip this and jump into interpreting the \(p\)-value. If you’re curious, we have included a discussion of this standardized t-test statistic in Subsection 9.5.

9.2.3 p-value

The fifth column of the regression table in Table 9.1 p_value corresponds to the p-value of the hypothesis test \(H_0: \beta_1 = 0\) versus \(H_A: \beta_1 \neq 0\).

Again recalling our terminology, notation, and definitions related to hypothesis tests we introduced in Section 7.2, let’s focus on the definition of the \(p\)-value:

A p-value is the probability of obtaining a test statistic just as extreme or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true.

Recall that you can intuitively think of the \(p\)-value as quantifying how “extreme” the observed fitted slope of \(b_1\) = 0.059 is in a “hypothesized universe” where there is no relationship between black nose proportions and lion ages.

Following the hypothesis testing procedure we outlined in Section 7.4, since the \(p\)-value in this case is 0, for any choice of significance level \(\alpha\) we would reject \(H_0\) in favor of \(H_A\). Using non-statistical language, this is saying: we reject the hypothesis that there is no relationship between black nose proportions and lion ages in favor of the hypothesis that there is. That is to say, the evidence suggests there is a significant relationship, one that is positive.

More precisely, however, the \(p\)-value corresponds to how extreme the observed test statistic of 7.053 is when compared to the appropriate null distribution. In Section 9.4, we’ll perform a simulation using the infer package to construct the null distribution in this case.

An extra caveat here is that the results of this hypothesis test are only valid if certain “conditions for inference for regression” are met, which we’ll introduce shortly in Section 9.3.

9.2.4 Confidence interval

The two rightmost columns of the regression table in Table 9.1 (lower_ci and upper_ci) correspond to the endpoints of the 95% confidence interval for the population slope \(\beta_1\). Recall our analogy of “nets are to fish” what “confidence intervals are to population parameters” from Section 6.3. The resulting 95% confidence interval for \(\beta_1\) of (0.042, 0.076) can be thought of as a range of plausible values for the population slope \(\beta_1\) of the linear relationship between black nose proportions and lion ages.

As we introduced in Subsection 6.5.2 on the precise and shorthand interpretation of confidence intervals, the statistically precise interpretation of this confidence interval is: “if we repeated this sampling procedure a large number of times, we expect about 95% of the resulting confidence intervals to capture the value of the population slope \(\beta_1\).” However, we’ll summarize this using our shorthand interpretation that “we’re 95% ‘confident’ that the true population slope \(\beta_1\) lies between 0.042 and 0.076.”

Notice in this case that the resulting 95% confidence interval for \(\beta_1\) of \((0.042, \, 0.076)\) does not contain a very particular value: \(\beta_1\) equals 0. Recall we mentioned that if the population regression slope \(\beta_1\) is 0, this is equivalent to saying there is no relationship between black nose proportions and lion ages. Since \(\beta_1\) = 0 is not in our plausible range of values for \(\beta_1\), we are inclined to believe that there, in fact, is a relationship between black nose proportions and lion ages and a positive one at that. So in this case, the conclusion about the population slope \(\beta_1\) from the 95% confidence interval matches the conclusion from the hypothesis test: evidence suggests that there is a meaningful relationship between black nose proportions and lion ages.

Recall from Subsection 6.5.3, however, that the confidence level is one of many factors that determine confidence interval widths. So for example, say we used a higher confidence level of 99% instead of 95%. The resulting confidence interval for \(\beta_1\) would be wider and thus might now include 0. The lesson to remember here is that any confidence-interval-based conclusion depends highly on the confidence level used.

What are the calculations that went into computing the two endpoints of the 95% confidence interval for \(\beta_1\)?

Recall our sampling bowl example from Subsection 6.8 discussing lower_ci and upper_ci. Since the sampling and bootstrap distributions of the sample proportion \(\widehat{p}\) were roughly normal, we could use the rule of thumb for bell-shaped distributions from Appendix A.2 to create a 95% confidence interval for \(p\) with the following equation, where MoE is the margin of error:

\[\widehat{p} \pm \text{MoE}_{\widehat{p}} = \widehat{p} \pm 1.96 \cdot \text{SE}_{\widehat{p}} = \widehat{p} \pm 1.96 \cdot \sqrt{\frac{\widehat{p}(1-\widehat{p})}{n}}\]

We can generalize this to other point estimates that have roughly normally shaped sampling and/or bootstrap distributions:

\[\text{point estimate} \pm \text{MoE} = \text{point estimate} \pm 1.96 \cdot \text{SE}.\]

We’ll show in Section 9.4 that the sampling/bootstrap distribution for the fitted slope \(b_1\) is in fact bell-shaped as well. Thus we can construct a 95% confidence interval for \(\beta_1\) with the following equation:

\[b_1 \pm \text{MoE}_{b_1} = b_1 \pm 1.96 \cdot \text{SE}_{b_1}.\]

What is the value of the standard error \(\text{SE}_{b_1}\)? It is in fact in the third column of the regression table in Table 9.1: 0.008. Thus

\[ \begin{aligned} b_1 \pm 1.96 \cdot \text{SE}_{b_1} &= 0.059 \pm 1.96 \cdot 0.008 = 0.059 \pm 0.016\\ &= (0.043, 0.075) \end{aligned} \]

This closely matches the \((0.042, 0.076)\) confidence interval in the last two columns of Table 9.1.

Much like hypothesis tests, however, the results of this confidence interval also are only valid if the “conditions for inference for regression” to be discussed in Section 9.3 are met.

9.2.5 How does R compute the table?

Since we didn’t perform the simulation to get the values of the standard error, test statistic, \(p\)-value, and endpoints of the 95% confidence interval in Table 9.1, you might be wondering how were these values computed. What did R do behind the scenes? Does R run simulations like we did using the infer package in Chapters 6 and 7 on confidence intervals and hypothesis testing?

The answer is no! Much like the theory-based method for constructing confidence intervals you saw in Subsection 6.8 and the theory-based hypothesis test you saw in Subsection 7.6, there exist mathematical formulas that allow you to construct confidence intervals and conduct hypothesis tests for inference for regression. These formulas were derived in a time when computers didn’t exist, so it would’ve been impossible to run the extensive computer simulations we have in this book. We present these formulas in Subsection 9.5 on “theory-based inference for regression.”

In Section 9.4, we’ll go over a simulation-based approach to constructing confidence intervals and conducting hypothesis tests using the infer package. In particular, we’ll convince you that the bootstrap distribution of the fitted slope \(b_1\) is indeed bell-shaped.

9.3 Conditions for inference for regression

Recall in Subsection 6.3.2 we stated that we could only use the standard-error-based method for constructing confidence intervals if the bootstrap distribution was bell shaped. Similarly, there are certain conditions that need to be met in order for the results of our hypothesis tests and confidence intervals we described in Section 9.2 to have valid meaning. These conditions must be met for the assumed underlying mathematical and probability theory to hold true.

For inference for regression, there are four conditions that need to be met. Note the first four letters of these conditions are highlighted in bold in what follows: LINE. This can serve as a nice reminder of what to check for whenever you perform linear regression.

1. Linearity of relationship between variables
2. Independence of the residuals
3. Normality of the residuals
4. Equality of variance of the residuals

Conditions L, N, and E can be verified through what is known as a residual analysis. Condition I can only be verified through an understanding of how the data was collected.

In this section, we’ll go over a refresher on residuals, verify whether each of the four LINE conditions hold true, and then discuss the implications.

9.3.1 Residuals refresher

Recall our definition of a residual from Subsection 8.1.3: it is the observed value minus the fitted value denoted by \(y - \widehat{y}\). Recall that residuals can be thought of as the error or the “lack-of-fit” between the observed value \(y\) and the fitted value \(\widehat{y}\) on the regression line in Figure 9.1. In Figure 9.2, we illustrate one particular residual out of 32 using an arrow, as well as its corresponding observed and fitted values using a circle and a square, respectively.

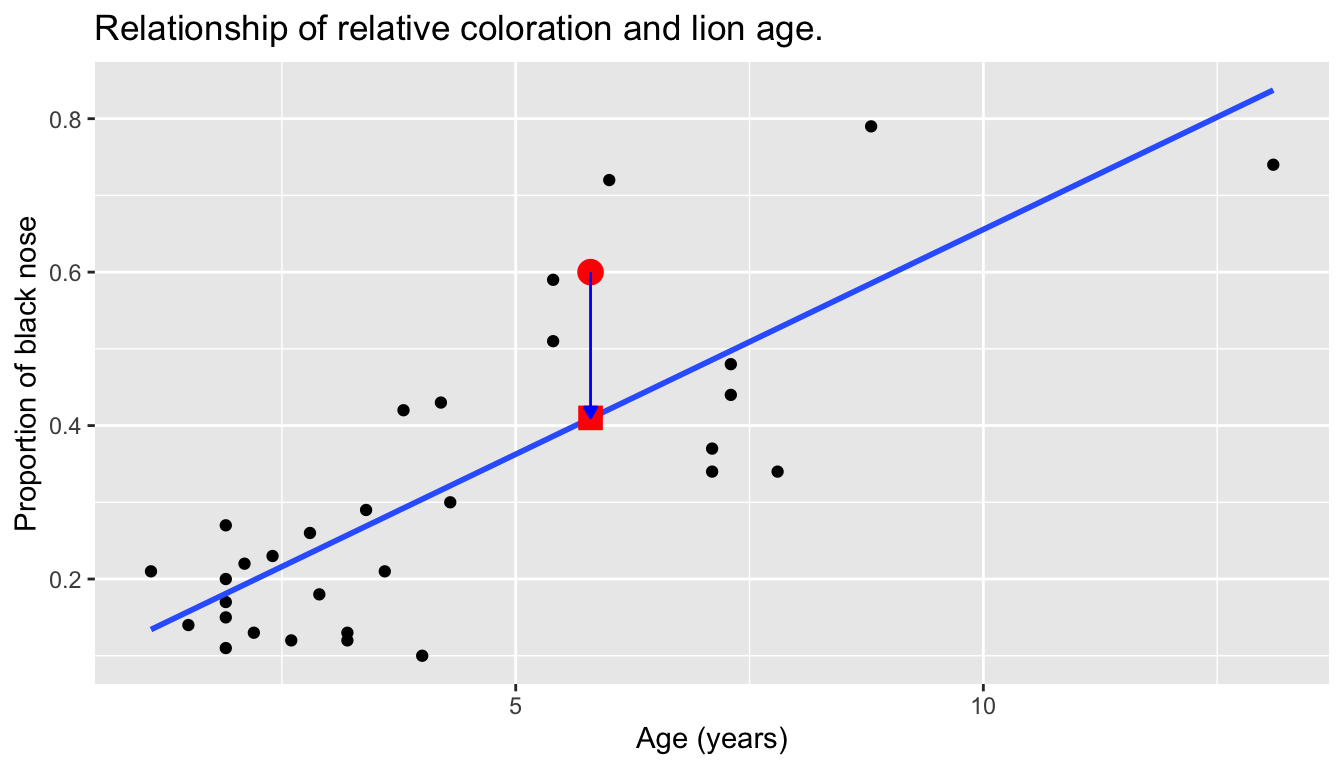
FIGURE 9.2: Example of observed value, fitted value, and residual.

Furthermore, we can automate the calculation of all \(n\) = 32 residuals by applying the get_regression_points() function to our saved regression model in lion_model. Observe how the resulting values of residual are roughly equal to proportion.black - proportion.black_hat (there is potentially a slight difference due to rounding error).

# Fit regression model:
lion_model <- lm(proportion.black ~ age, data = LionNoses)
# Get regression points:
regression_points <- get_regression_points(lion_model)
regression_points

# A tibble: 32 × 5
      ID proportion.black   age proportion.black_hat residual
   <int>            <dbl> <dbl>                <dbl>    <dbl>
 1     1             0.21   1.1                0.134    0.076
 2     2             0.14   1.5                0.158   -0.018
 3     3             0.11   1.9                0.181   -0.071
 4     4             0.13   2.2                0.199   -0.069
 5     5             0.12   2.6                0.222   -0.102
 6     6             0.13   3.2                0.257   -0.127
 7     7             0.12   3.2                0.257   -0.137
 8     8             0.18   2.9                0.24    -0.06 
 9     9             0.23   2.4                0.21     0.02 
10    10             0.22   2.1                0.193    0.027
# ℹ 22 more rows

A residual analysis is used to verify conditions L, N, and E and can be performed using appropriate data visualizations. While there are more sophisticated statistical approaches that can also be done, we’ll focus on the much simpler approach of looking at plots.

9.3.2 Linearity of relationship

The first condition is that the relationship between the outcome variable \(y\) and the explanatory variable \(x\) must be Linear. Recall the scatterplot in Figure 9.1 where we had the explanatory variable \(x\) as lion age and the outcome variable \(y\) as proportion.black. Would you say that the relationship between \(x\) and \(y\) is linear? It’s hard to say because of the scatter of the points about the line, but in the authors’ opinions, this relationship is “linear enough.”

Let’s present an example where the relationship between \(x\) and \(y\) is clearly not linear in Figure 9.3. In this case, the points clearly do not form a line, but rather a U-shaped polynomial curve. In this case, any results from an inference for regression would not be valid.

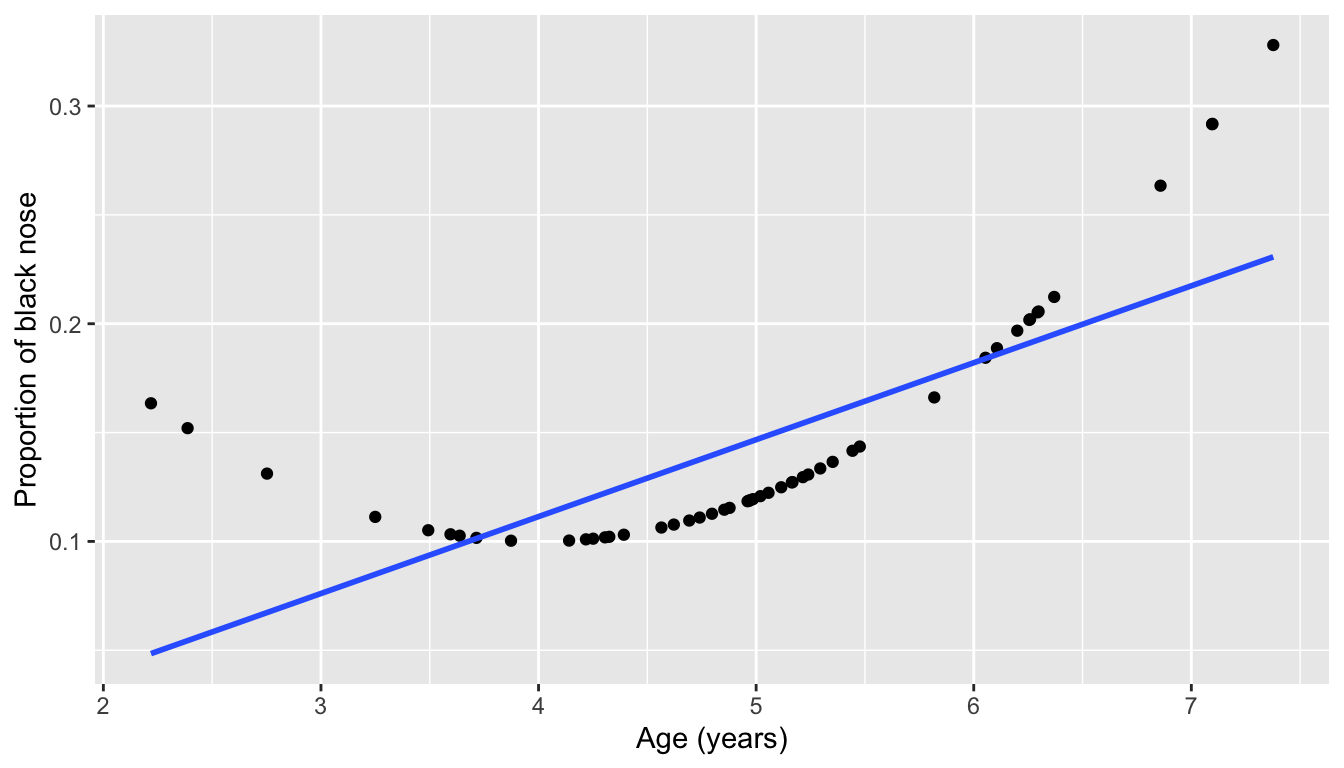
FIGURE 9.3: Example of a clearly non-linear relationship.

9.3.3 Independence of residuals

The second condition is that the residuals must be Independent. In other words, the different observations in our data must be independent of one another. Presumably, the observations are independent, but without further details about how the study was conducted, we can’t be certain. For example, if the black nose proportion of the same lion was measured multiple times at different ages, then there would be dependence between those observations. If this was the case, a proper analysis of the data would need to take into account that we have repeated measures for the same lions. We’ll presume, however, that the observations are independent of each other.

9.3.4 Normality of residuals

The third condition is that the residuals should follow a Normal distribution. Furthermore, the center of this distribution should be 0. In other words, sometimes the regression model will make positive errors: \(y - \widehat{y} > 0\). Other times, the regression model will make equally negative errors: \(y - \widehat{y} < 0\). However, on average the errors should equal 0 and their shape should be similar to that of a bell.

The simplest way to check the normality of the residuals is to look at a histogram, which we visualize in Figure 9.4.

ggplot(regression_points, aes(x = residual)) +
  geom_histogram(binwidth = 0.05, color = "white") +
  labs(x = "Residual")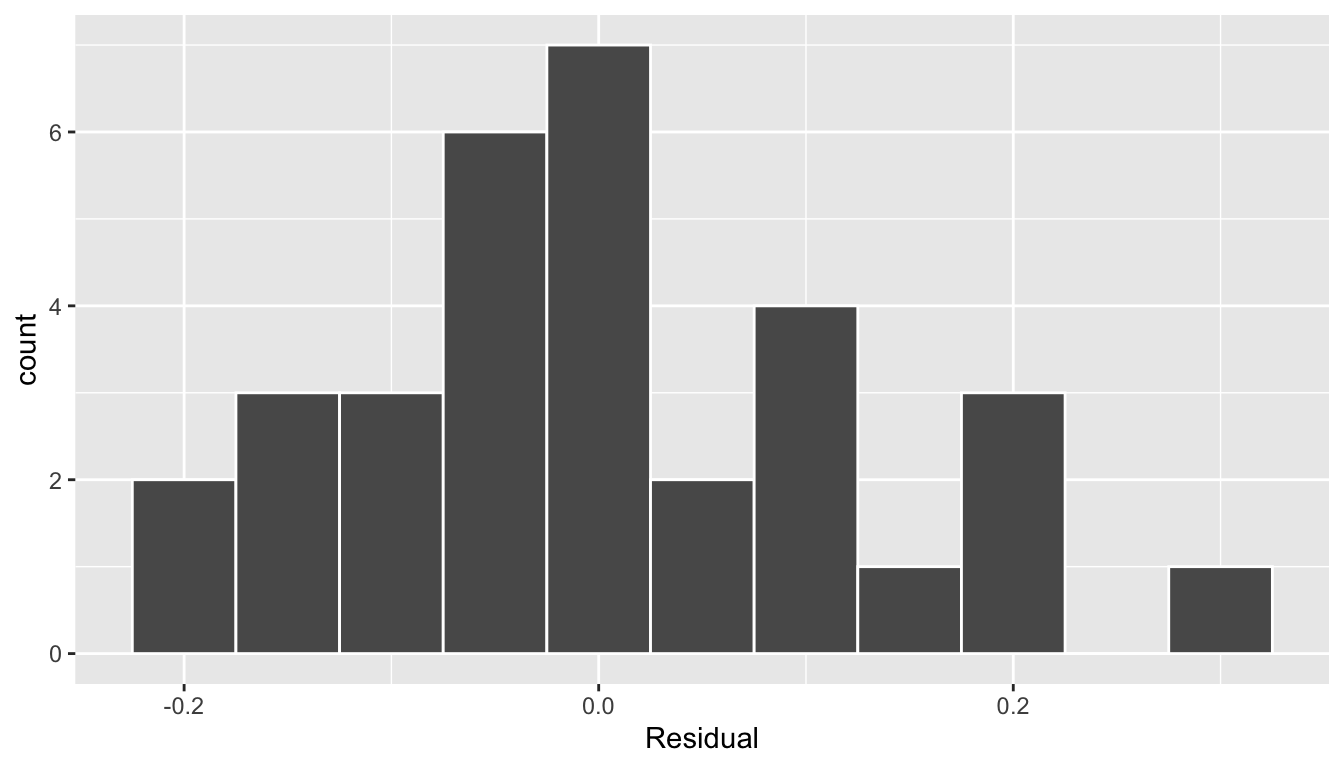

FIGURE 9.4: Histogram of residuals.

This histogram shows that we have more negative residuals than positive. Since the residual \(y-\widehat{y}\) is positive when \(y > \widehat{y}\), it seems our regression model’s fitted black nose proportions \(\widehat{y}\) tend to overestimate the true proportion.black \(y\). Furthermore, this histogram has a slight right-skew in that there is a tail on the right. This is another way to say the residuals exhibit a positive skew.

Is this a problem? Again, there is a certain amount of subjectivity in the response. In the authors’ opinion, while there is a slight skew to the residuals, we feel it isn’t drastic. On the other hand, others might disagree with our assessment.

Let’s present examples where the residuals clearly do and don’t follow a normal distribution in Figure 9.5. In this case of the model yielding the clearly non-normal residuals on the right, any results from an inference for regression would not be valid.

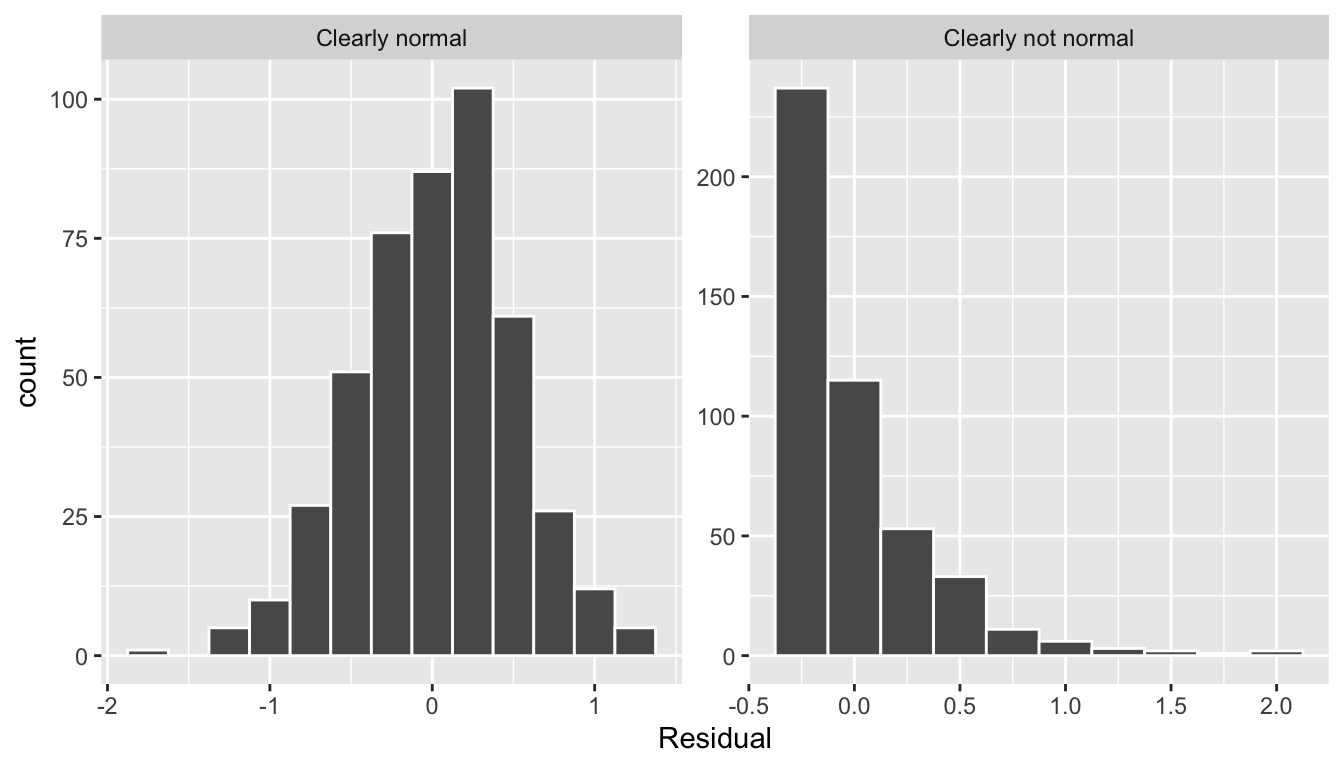
FIGURE 9.5: Example of clearly normal and clearly not normal residuals.

9.3.5 Equality of variance

The fourth and final condition is that the residuals should exhibit Equal variance across all values of the explanatory variable \(x\). In other words, the value and spread of the residuals should not depend on the value of the explanatory variable \(x\).

Recall the scatterplot in Figure 9.1: we had the explanatory variable \(x\) of age on the x-axis and the outcome variable \(y\) of proportion.black on the y-axis. Instead, let’s create a scatterplot that has the same values on the x-axis, but now with the residual \(y-\widehat{y}\) on the y-axis as seen in Figure 9.6.

ggplot(regression_points, aes(x = age, y = residual)) +
  geom_point() +
  labs(x = "Age (years)", y = "Residual") +
  geom_hline(yintercept = 0, col = "blue", size = 1)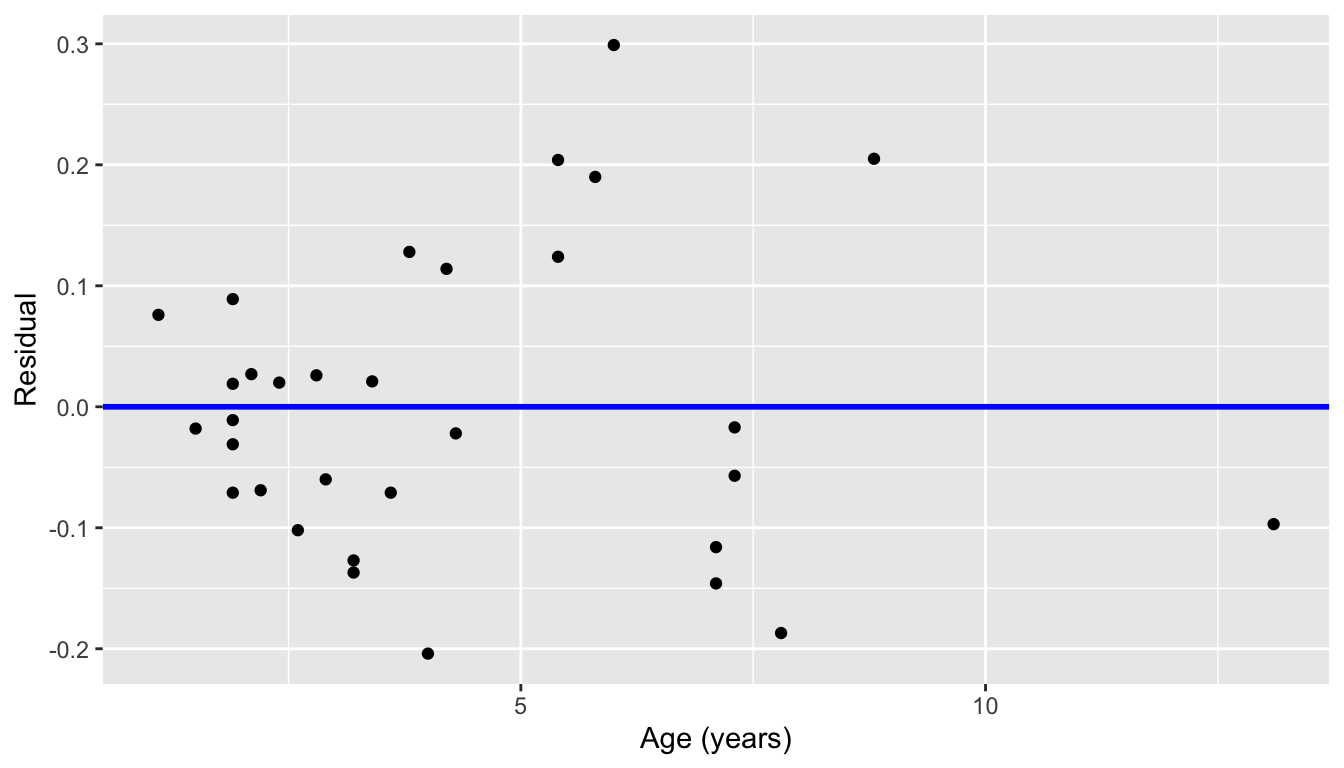

FIGURE 9.6: Plot of residuals over age.

You can think of Figure 9.6 as a modified version of the plot with the regression line in Figure 9.1, but with the regression line flattened out to \(y=0\). Looking at this plot, would you say that the spread of the residuals around the line at \(y=0\) is constant across all values of the explanatory variable \(x\) of age? This question is rather qualitative and subjective in nature, thus different people may respond with different answers. For example, some people might say that there is slightly less variation in the residuals for smaller values of \(x\) than for middle ones. However, it can be argued that there isn’t a drastic non-constancy.

In Figure 9.7 let’s present an example where the residuals clearly do not have equal variance across all values of the explanatory variable \(x\).

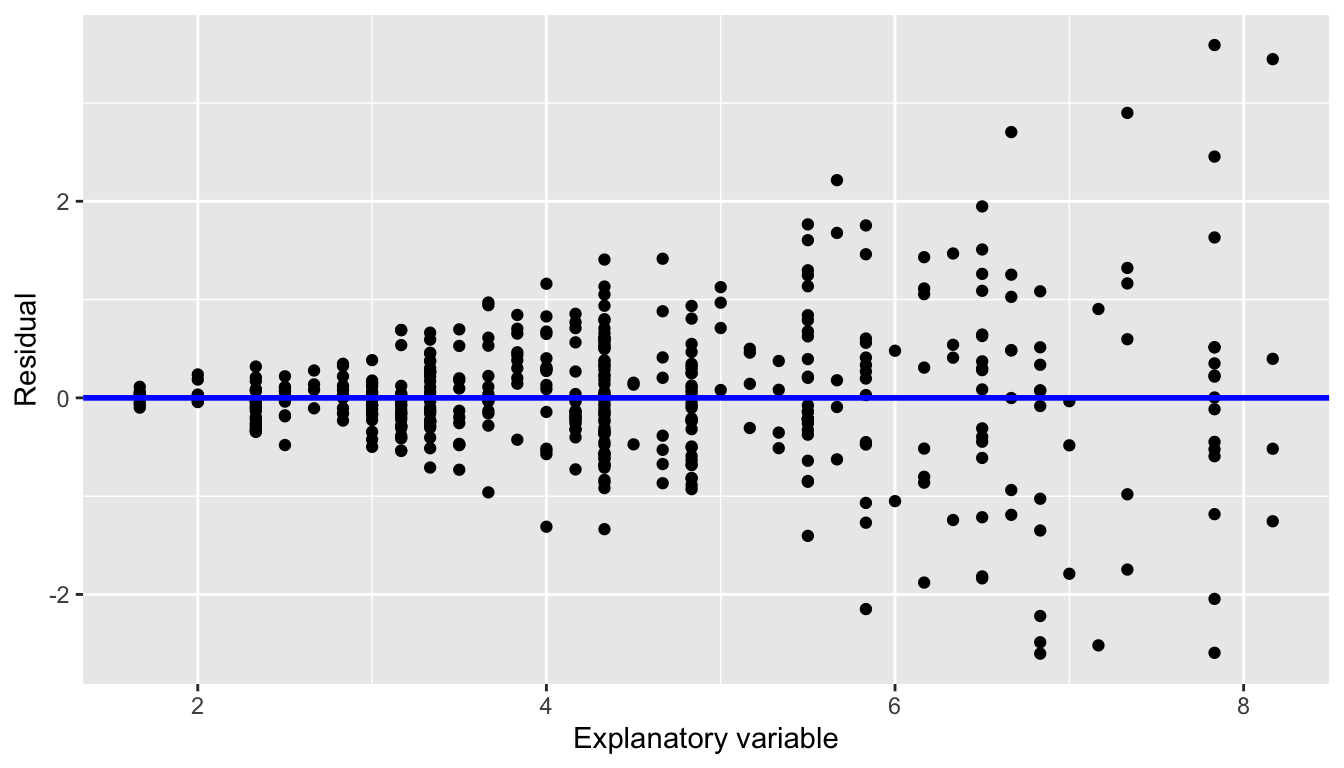
FIGURE 9.7: Example of clearly non-equal variance.

Observe how the spread of the residuals increases as the value of \(x\) increases. This is a situation known as heteroskedasticity. Any inference for regression based on a model yielding such a pattern in the residuals would not be valid.

9.3.6 What’s the conclusion?

Let’s list our four conditions for inference for regression again and indicate whether or not they were satisfied in our analysis:

1. Linearity of relationship between variables: Yes
2. Independence of residuals: Presumably
3. Normality of residuals: Somewhat
4. Equality of variance: Yes

So what does this mean for the results of our confidence intervals and hypothesis tests in Section 9.2?

First, the Independence condition. Since the observations are presumably independent, we can proceed. If there had been dependencies between different rows in LionNoses, then we would need to address this. In more advanced statistics courses, you’ll learn how to incorporate such dependencies into your regression models. One such technique is called hierarchical/multilevel modeling.

Second, when conditions L, N, E are not met, it often means there is a shortcoming in our model. For example, it may be the case that using only a single explanatory variable is insufficient, as we did with proportion.black. We may need to incorporate more explanatory variables in a multiple regression model as we did in Chapter 10.

The conditions for inference in regression problems are a key part of regression analysis that are of vital importance to the processes of constructing confidence intervals and conducting hypothesis tests. However, it is often the case with regression analysis in the real world that not all the conditions are completely met. Furthermore, as you saw, there is a level of subjectivity in the residual analyses to verify the L, N, and E conditions. So what can you do? We as authors advocate for transparency in communicating all results. This lets the stakeholders of any analysis know about a model’s shortcomings or whether the model is “good enough.” So while the checking of assumptions may lead to some fuzzy “it depends” results, you should be prepared for difficult statistical decisions you may need to make down the road.

Learning check

(LC9.1) Continuing with our regression using age as the explanatory variable and proportion.black as the outcome variable.

• Use the get_regression_points() function to get the observed values, fitted values, and residuals for all 32 lions
• Perform a residual analysis and look for any systematic patterns in the residuals. Ideally, there should be little to no pattern but comment on what you find here.

9.4 Simulation-based inference for regression

Recall in Subsection 9.2.5 when we interpreted the third through seventh columns of a regression table, we stated that R doesn’t do simulations to compute these values. Rather R uses theory-based methods that involve mathematical formulas.

In this section, we’ll use the simulation-based methods you previously learned in Chapters 6 and 7 to recreate the values in the regression table in Table 9.1. In particular, we’ll use the infer package workflow to

• Construct a 95% confidence interval for the population slope \(\beta_1\) using bootstrap resampling with replacement. We did this previously in Sections 6.4 with the pennies data and 6.6 with the mythbusters_yawn data.
• Conduct a hypothesis test of \(H_0: \beta_1 = 0\) versus \(H_A: \beta_1 \neq 0\) using a permutation test. We did this previously in Sections 7.3 with the BirdMalaria data and 7.5 with the HornedLizards data.

9.4.1 Confidence interval for slope

We’ll construct a 95% confidence interval for \(\beta_1\) using the infer workflow outlined in Subsection 6.4.2. Specifically, we’ll first construct the bootstrap distribution for the fitted slope \(b_1\) using our single sample of 32 lions:

1. specify() the variables of interest in LionNoses with the formula: proportion.black ~ age.
2. generate() replicates by using bootstrap resampling with replacement from the original sample of 32 lions. We generate reps = 1000 replicates using type = "bootstrap".
3. calculate() the summary statistic of interest: the fitted slope \(b_1\).

Using this bootstrap distribution, we’ll construct the 95% confidence interval using the percentile method and (if appropriate) the standard error method as well. It is important to note in this case that the bootstrapping with replacement is done row-by-row. Thus, the original pairs of proportion.black and age values are always kept together, but different pairs of proportion.black and age values may be resampled multiple times. The resulting confidence interval will denote a range of plausible values for the unknown population slope \(\beta_1\) quantifying the relationship between black nose proportions and lion ages for all lions in this wild population.

Let’s first construct the bootstrap distribution for the fitted slope \(b_1\):

bootstrap_distn_slope <- LionNoses %>% 
  specify(formula = proportion.black ~ age) %>%
  generate(reps = 1000, type = "bootstrap") %>% 
  calculate(stat = "slope")
bootstrap_distn_slope

# A tibble: 1,000 × 2
   replicate      stat
       <int>     <dbl>
 1         1 0.0651055
 2         2 0.0382313
 3         3 0.108056 
 4         4 0.0666601
 5         5 0.0715932
 6         6 0.0854565
 7         7 0.0624868
 8         8 0.0412859
 9         9 0.0796269
10        10 0.0761299
# ℹ 990 more rows

Observe how we have 1000 values of the bootstrapped slope \(b_1\) in the stat column. Let’s visualize the 1000 bootstrapped values in Figure 9.8.

visualize(bootstrap_distn_slope)

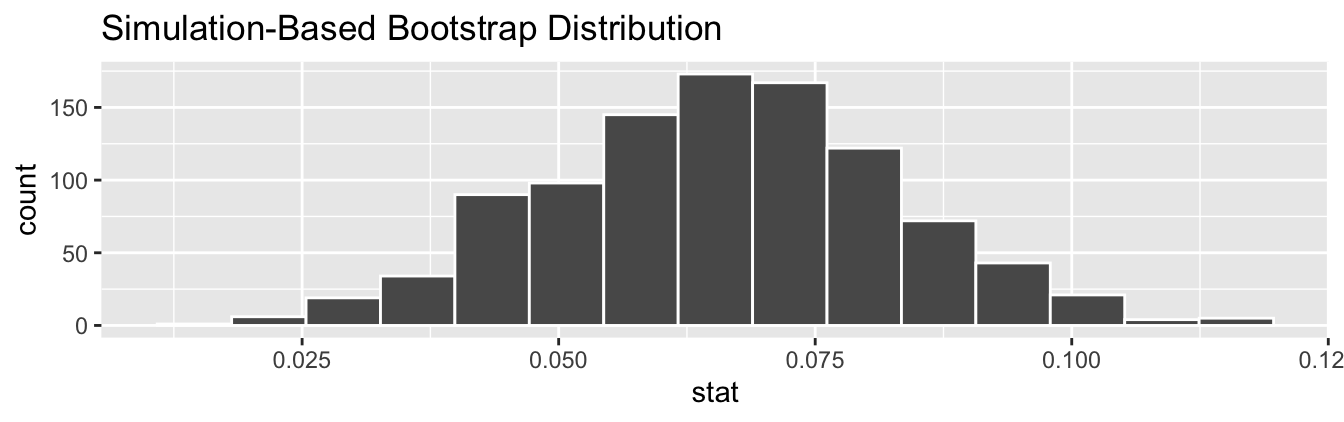
FIGURE 9.8: Bootstrap distribution of slope.

Observe how the bootstrap distribution is roughly bell-shaped. Recall from Subsection 6.7 that the shape of the bootstrap distribution of \(b_1\) closely approximates the shape of the sampling distribution of \(b_1\).

Percentile-method

First, let’s compute the 95% confidence interval for \(\beta_1\) using the percentile method. We’ll do so by identifying the 2.5th and 97.5th percentiles which include the middle 95% of values. Recall that this method does not require the bootstrap distribution to be normally shaped.

percentile_ci <- bootstrap_distn_slope %>% 
  get_confidence_interval(type = "percentile", level = 0.95)
percentile_ci

# A tibble: 1 × 2
   lower_ci  upper_ci
      <dbl>     <dbl>
1 0.0323411 0.0990027

The resulting percentile-based 95% confidence interval for \(\beta_1\) of (0.032, 0.099) is similar to the confidence interval in the regression Table 9.1 of (0.042, 0.076).

Standard error method

Since the bootstrap distribution in Figure 9.8 appears to be roughly bell-shaped, we can also construct a 95% confidence interval for \(\beta_1\) using the standard error method.

In order to do this, we need to first compute the fitted slope \(b_1\), which will act as the center of our standard error-based confidence interval. While we saw in the regression table in Table 9.1 that this was \(b_1\) = 0.059, we can also use the infer pipeline with the generate() step removed to calculate it:

observed_slope <- LionNoses %>% 
  specify(proportion.black ~ age) %>% 
  calculate(stat = "slope")
observed_slope

Response: proportion.black (numeric)
Explanatory: age (numeric)
# A tibble: 1 × 1
       stat
      <dbl>
1 0.0585912

We then use the get_ci() function with level = 0.95 to compute the 95% confidence interval for \(\beta_1\). Note that setting the point_estimate argument to the observed_slope of 0.059 sets the center of the confidence interval.

se_ci <- bootstrap_distn_slope %>% 
  get_ci(level = 0.95, type = "se", point_estimate = observed_slope)
se_ci

# A tibble: 1 × 2
   lower_ci  upper_ci
      <dbl>     <dbl>
1 0.0253308 0.0918515

The resulting standard error-based 95% confidence interval for \(\beta_1\) of \((0.025, 0.092)\) is slightly different than the confidence interval in the regression Table 9.1 of \((0.042, 0.076)\).

Comparing all three

Let’s compare all three confidence intervals in Figure 9.9, where the percentile-based confidence interval is marked with solid lines, the standard error based confidence interval is marked with dashed lines, and the theory-based confidence interval (0.042, 0.076) from the regression table in Table 9.1 is marked with dotted lines.

visualize(bootstrap_distn_slope) + 
  shade_confidence_interval(endpoints = percentile_ci, fill = NULL, 
                            linetype = "solid", color = "grey90") + 
  shade_confidence_interval(endpoints = se_ci, fill = NULL, 
                            linetype = "dashed", color = "grey60") +
  shade_confidence_interval(endpoints = c(0.035, 0.099), fill = NULL, 
                            linetype = "dotted", color = "black")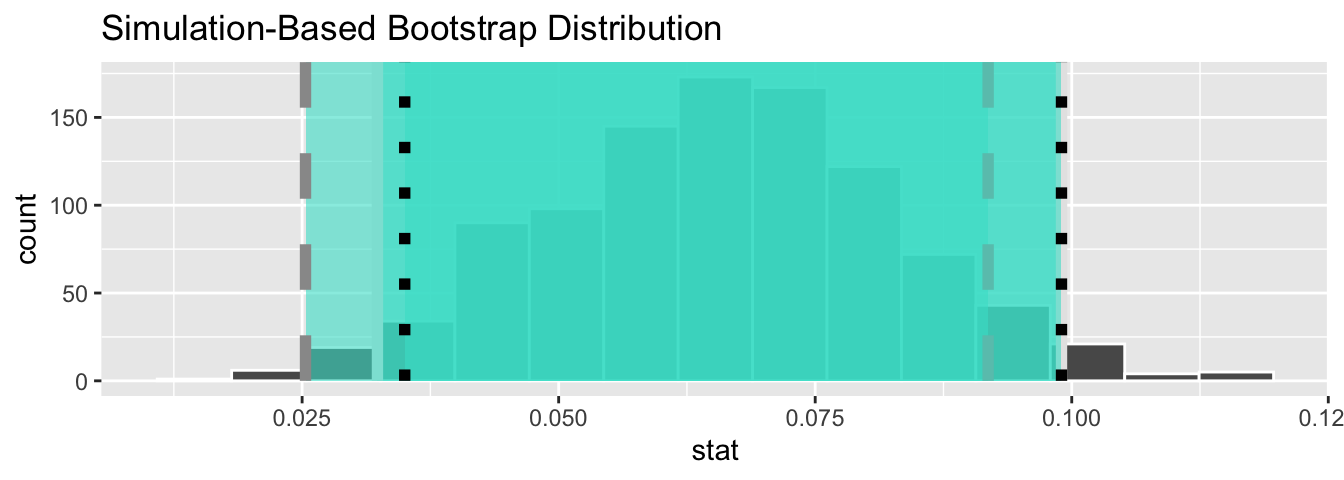

FIGURE 9.9: Comparing three confidence intervals for the slope.

Observe that all three are quite similar! Furthermore, none of the three confidence intervals for \(\beta_1\) contain 0 and are entirely located above 0. This is suggesting that there is in fact a meaningful positive relationship between black nose proportions and lion ages.

9.4.2 Hypothesis test for slope

Let’s now conduct a hypothesis test of \(H_0: \beta_1 = 0\) vs. \(H_A: \beta_1 \neq 0\). We will use the infer package, which follows the hypothesis testing paradigm in the “There is only one test” diagram in Figure 7.14.

Let’s first think about what it means for \(\beta_1\) to be zero as assumed in the null hypothesis \(H_0\). Recall we said if \(\beta_1 = 0\), then this is saying there is no relationship between the black nose proportions and lion ages. Thus assuming this particular null hypothesis \(H_0\) means that in our “hypothesized universe” there is no relationship between proportion.black and age. We can therefore shuffle/permute the age variable to no consequence.

We construct the null distribution of the fitted slope \(b_1\) by performing the steps that follow. Recall from Section 7.2 on terminology, notation, and definitions related to hypothesis testing where we defined the null distribution: the sampling distribution of our test statistic \(b_1\) assuming the null hypothesis \(H_0\) is true.

1. specify() the variables of interest in LionNoses with the formula: proportion.black ~ age.
2. hypothesize() the null hypothesis of independence. Recall from Section 7.3 that this is an additional step that needs to be added for hypothesis testing.
3. generate() replicates by permuting/shuffling values from the original sample of 32 courses. We generate reps = 1000 replicates using type = "permute" here.
4. calculate() the test statistic of interest: the fitted slope \(b_1\).

In this case, we permute the values of age across the values of proportion.black 1000 times. We can do this shuffling/permuting since we assumed a “hypothesized universe” of no relationship between these two variables. Then we calculate the "slope" coefficient for each of these 1000 generated samples.

null_distn_slope <- LionNoses %>% 
  specify(proportion.black ~ age) %>%
  hypothesize(null = "independence") %>% 
  generate(reps = 1000, type = "permute") %>% 
  calculate(stat = "slope")

Observe the resulting null distribution for the fitted slope \(b_1\) in Figure 9.10.

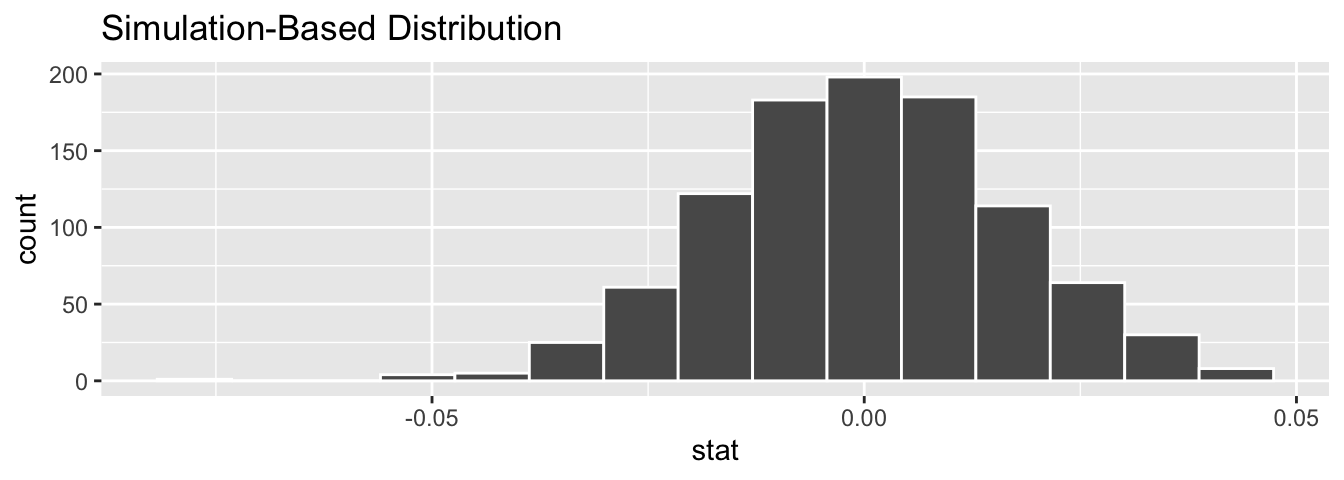
FIGURE 9.10: Null distribution of slopes.

Notice how it is centered at \(b_1\) = 0. This is because in our hypothesized universe, there is no relationship between proportion.black and age and so \(\beta_1 = 0\). Thus, the most typical fitted slope \(b_1\) we observe across our simulations is 0. Observe, furthermore, how there is variation around this central value of 0.

Let’s visualize the \(p\)-value in the null distribution by comparing it to the observed test statistic of \(b_1\) = 0.059 in Figure 9.11. We’ll do this by adding a shade_p_value() layer to the previous visualize() code.

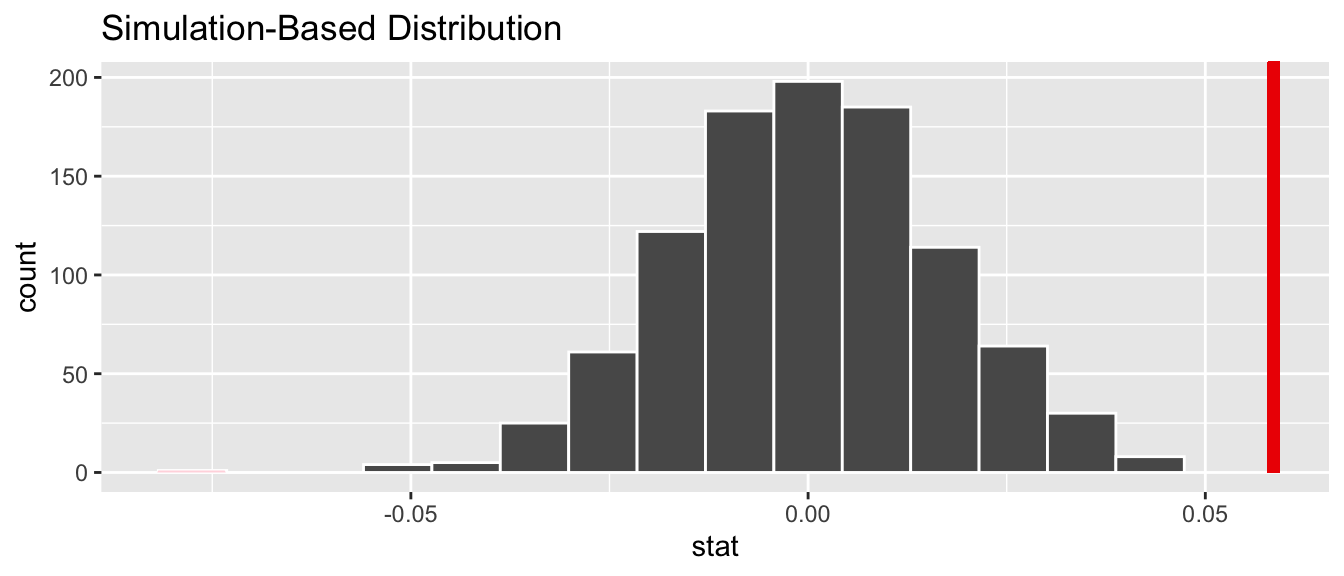
FIGURE 9.11: Null distribution and \(p\)-value.

Since the observed fitted slope 0.059 falls far to the right of this null distribution and thus the shaded region doesn’t overlap it, we’ll have a \(p\)-value of 0. For completeness, however, let’s compute the numerical value of the \(p\)-value anyways using the get_p_value() function. Recall that it takes the same inputs as the shade_p_value() function:

null_distn_slope %>% 
  get_p_value(obs_stat = observed_slope, direction = "both")

# A tibble: 1 × 1
  p_value
    <dbl>
1       0

This matches the \(p\)-value of 0 in the regression table in Table 9.1. We therefore reject the null hypothesis \(H_0: \beta_1 = 0\) in favor of the alternative hypothesis \(H_A: \beta_1 \neq 0\). We thus have evidence that suggests there is a significant relationship between black nose proportions and lion ages for all lions in this population.

When the conditions for inference for regression are met and the null distribution has a bell shape, we are likely to see similar results between the simulation-based results we just demonstrated and the theory-based results shown in the regression table in Table 9.1.

Learning check

(LC9.2) Repeat the inference but this time for the correlation coefficient instead of the slope. Note the implementation of stat = "correlation" in the calculate() function of the infer package.

9.5 Theory-based inference for regression

Recall in Subsection 9.2.5 when we interpreted the regression table in Table 9.1, we mentioned that R does not compute its values using simulation-based methods for constructing confidence intervals and conducting hypothesis tests as we did in Chapters 6 and 7 using the infer package. Rather, R uses a theory-based approach using mathematical formulas, much like the theory-based confidence intervals you saw in Subsection 6.8 and the theory-based hypothesis tests you saw in Subsection 7.6. These formulas were derived in a time when computers didn’t exist, so it would’ve been incredibly labor intensive to run extensive simulations.

In particular, there is a formula for the standard error of the fitted slope \(b_1\):

\[\text{SE}_{b_1} = \dfrac{\dfrac{s_y}{s_x} \cdot \sqrt{1-r^2}}{\sqrt{n-2}}\]

As with many formulas in statistics, there’s a lot going on here, so let’s first break down what each symbol represents. First \(s_x\) and \(s_y\) are the sample standard deviations of the explanatory variable age and the response variable proportion.black, respectively. Second, \(r\) is the sample correlation coefficient between proportion.black and age. This was computed as 0.79 in Chapter 8. Lastly, \(n\) is the number of pairs of points in the LionNoses data frame, here 32.

To put this formula into words, the standard error of \(b_1\) depends on the relationship between the variability of the response variable and the variability of the explanatory variable as measured in the \(s_y / s_x\) term. Next, it looks into how the two variables relate to each other in the \(\sqrt{1-r^2}\) term.

However, the most important observation to make in the previous formula is that there is an \(n - 2\) in the denominator. In other words, as the sample size \(n\) increases, the standard error \(\text{SE}_{b_1}\) decreases. Just as we demonstrated in Subsection 5.3.3 when we used shovels with \(n\) = 25, 50, and 100 slots, the amount of sampling variation of the fitted slope \(b_1\) will depend on the sample size \(n\). In particular, as the sample size increases, both the sampling and bootstrap distributions narrow and the standard error \(\text{SE}_{b_1}\) decreases. Hence, our estimates of \(b_1\) for the true population slope \(\beta_1\) get more and more precise.

R then uses this formula for the standard error of \(b_1\) in the third column of the regression table and subsequently to construct 95% confidence intervals. But what about the hypothesis test? Much like with our theory-based hypothesis test in Subsection 7.6, R uses the following \(t\)-statistic as the test statistic for hypothesis testing:

\[ t = \dfrac{ b_1 - \beta_1}{ \text{SE}_{b_1}} \]

And since the null hypothesis \(H_0: \beta_1 = 0\) is assumed during the hypothesis test, the \(t\)-statistic becomes

\[ t = \dfrac{ b_1 - 0}{ \text{SE}_{b_1}} = \dfrac{ b_1 }{ \text{SE}_{b_1}} \]

What are the values of \(b_1\) and \(\text{SE}_{b_1}\)? They are in the estimate and std_error column of the regression table in Table 9.1. Thus the value of 7.053 in the table is computed as 0.059/0.008 = 7.375. Note there is a difference due to some rounding error here.

Lastly, to compute the \(p\)-value, we need to compare the observed test statistic of 7.053 to the appropriate null distribution. Recall from Section 7.2, that a null distribution is the sampling distribution of the test statistic assuming the null hypothesis \(H_0\) is true. Much like in our theory-based hypothesis test in Subsection 7.6, it can be mathematically proven that this distribution is a \(t\)-distribution with degrees of freedom equal to \(df = n - 2 = 32 - 2 = 30\).

Don’t worry if you’re feeling a little overwhelmed at this point. There is a lot of background theory to understand before you can fully make sense of the equations for theory-based methods. That being said, theory-based methods and simulation-based methods for constructing confidence intervals and conducting hypothesis tests often yield consistent results. As mentioned before, in our opinion, two large benefits of simulation-based methods over theory-based are that (1) they are easier for people new to statistical inference to understand, and (2) they also work in situations where theory-based methods and mathematical formulas don’t exist.

9.6 Conclusion

Chapter Learning Summary

• The fitted intercept and slope for a regression line based on a sample are point estimates of these values for the regression line of the population.
  
• The standard errors of the fitted intercept \(b_0\) and slope \(b_1\) quantify the sampling variability.
  
• The null hypothesis for linear regression is that the population slope \(B_1\) equals 0, indicating no relationship between the response and explanatory variables.
  
• Linear regression compares the observed standardized t-test statistic to its null distribution to determine the p-value.
  
• Linear regression uses the standard errors of \(b_0\) and \(b_1\) to calculate the confidence intervals of each coefficient.
  
• For linear regression results to be valid, the residuals must have a linear relationship, be independent, and have a normal distribution and equal variance across all \(x\) values (LINE).
  
• In addition to the theory-based method, computer-based methods can also be used to compute the p-value and 95% confidence interval for \(B_0\) and \(B_1\).
  

9.6.1 Summary of statistical inference

We’ve finished the last scenario from the “Scenarios of sampling for inference” table in Subsection 5.6, which we re-display in Table 9.4.

TABLE 9.4: Scenarios of sampling for inference

Scenario	Population parameter	Notation	Point estimate	Symbol(s)
1	Population proportion	\(p\)	Sample proportion	\(\widehat{p}\)
2	Population mean	\(\mu\)	Sample mean	\(\overline{x}\) or \(\widehat{\mu}\)
3	Difference in population proportions	\(p_1 - p_2\)	Difference in sample proportions	\(\widehat{p}_1 - \widehat{p}_2\)
4	Difference in population means	\(\mu_1 - \mu_2\)	Difference in sample means	\(\overline{x}_1 - \overline{x}_2\)
5	Population regression slope	\(\beta_1\)	Fitted regression slope	\(b_1\) or \(\widehat{\beta}_1\)

Armed with the regression modeling techniques you learned in Chapter 8, your understanding of sampling for inference in Chapter 5, and the tools for statistical inference like confidence intervals and hypothesis tests in Chapters 6 and 7, you’re now equipped to study the significance of relationships between variables in a wide array of data! Many of the ideas presented here can be extended into multiple regression, as we’ll see in Chapter 10 and other more advanced modeling techniques.

9.6.2 What’s to come

In Chapter 10, we’ll study multiple regression, where our regression models can now have more than one explanatory variable! In particular, we’ll consider two scenarios: regression models with one numerical and one categorical explanatory variable and regression models with two categorical explanatory variables. This will allow you to construct more sophisticated and more powerful models, all in the hopes of better explaining your outcome variable \(y\).